Hole in a Infinite Plate Subjected to Remote Stress: plateHole
Prepared by Philip Cardiff and Ivan Batistić
Tutorial Aims
- Demonstrate the solver accuracy for a linear elastic test case
Case Overview
In this case, a thin, infinitely large plate with a circular hole is subjected to uniaxial tension of \(\sigma_{xx} = T = 1\) MPa, see Figure 1. Owing to the symmetry of the geometry and loading, only one quarter of the plate is modelled. To minimise the influence of the finite computational boundaries, the exact tractions obtained from the analytical solution [1,2] are prescribed on the outer edges BC and CD. They are defined with analyticalPlateHoleTraction boundary conditions, which require geometry (hole radius) and loading (far-field traction):
right
{
type analyticalPlateHoleTraction;
farFieldTractionX 1e6;
holeRadius 0.5;
value uniform (0 0 0);
}
Symmetry boundary conditions are applied on boundaries AB and DE, while zero traction is specified on the hole boundary. The material properties are defined by a Young's modulus of \(E = 200 GPa\) and a Poisson's ratio of \(\nu = 0.3\). Gravitational and inertial effects are neglected, and the case is solved using one loading increment.
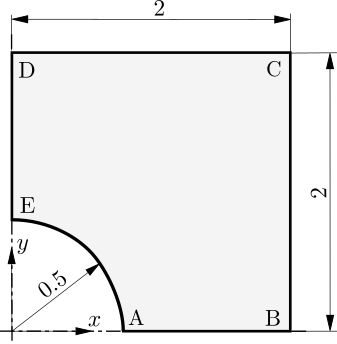
Figure 1 - Problem geometry [3]
Expected Results
The analytical solution for the stress field is [1,2]:
\[\sigma_{xx} = T \left[ 1 - \dfrac{R^2}{r^2} \left( \dfrac{3}{2}\cos(2\theta) +\cos (4\theta)\right) + \dfrac{3}{2}\dfrac{R^4}{r^4}\cos (4\theta) \right],\] \[\sigma_{yy} = T \left[ - \dfrac{R^2}{r^2} \left( \dfrac{1}{2}\cos(2\theta) -\cos (4\theta)\right) - \dfrac{3}{2}\dfrac{R^4}{r^4}\cos (4\theta) \right],\] \[\sigma_{xy} = T \left[ - \dfrac{R^2}{r^2} \left( \dfrac{1}{2}\sin(2\theta) +\sin (4\theta)\right) + \dfrac{3}{2}\dfrac{R^4}{r^4}\sin (4\theta) \right].\]where \(r=\sqrt{x^2+y^2}\) and \(\theta=\tan^{-1}(y/x)\) are the usual polar co-ordinates. \(R\) is the hole radius, .
A custom plateHoleAnalyticalSolution function object is added to the controlDict to calculate the analytical solutions for displacement and stress and compute the errors:
plateHoleAnalyticalSolution1
{
type plateHoleAnalyticalSolution;
farFieldTractionX 1e6; // Farfield sigma_xx
holeRadius 0.5; // Hole radius
E 200e+9; // Young modulus
nu 0.3; // Poissons ratio
}
The function object prints the average \(L_1\), \(L_2\), and \(L_\infty\) norms for the stress components (\(\sigma_{xx}\), \(\sigma_{yy}\), and \(\sigma_{xy}\)) and for the displacement field:
Writing cellStressDifference field
Component: 0
Norms: mean L1, mean L2, LInf:
3284.42 10421.2 105024
Component: 1
Norms: mean L1, mean L2, LInf:
2100.42 6111.58 59602.5
Component: 3
Norms: mean L1, mean L2, LInf:
2917.5 8547 87630.5
Writing DDifference field
Norms: mean L1, mean L2, LInf:
1.2549e-08 1.37329e-08 4.24642e-08
In solids4foam the error normas \(L_1\),\(L_2\) and \(L_\inf\) are defines as:
where \(\Delta \phi_i\) is the difference between expected and predicted solutions For variable \(\phi\) at computational nodes and \(N_{\text{c}}\) is the overall number of computational nodes, i.e. cells.
Running the Case
The tutorial case is located at solids4foam/tutorials/solids/linearElasticity/plateHole. The case can be run using the included Allrun script, i.e. > ./Allrun. In this case, the Allrun consists of creating the mesh using blockMesh (> ./blockMesh) followed by running the solids4foam solver (> ./solids4Foam) . Optionally, the case can be run in parallel using ./Allrun parallel