Stress relaxation of a viscoelastic tube: viscoTube
Prepared by Philip Cardiff and Ivan Batistić
Tutorial Aims
- Demonstrate a transient viscoelastic analysis;
- Compare viscoelastic predictions with a reference finite element solution.
Case Overview
This case consists of a tube constructed from a viscoelastic material [1], where the inner surface is quickly displaced in the radial direction; subsequently, the tube relaxes towards a steady state after initially experiencing high wall stresses. The case is modelled as 2-D with quarter symmetries, as schematically shown in Figure 1. The cylindrical tube has an inner radius of \(5\) mm and an outer radius of \(10\) mm. The tube material is assumed to be a viscoelastic polymer where a Prony series represents its deviatoric response, and its bulk/volumetric response is assumed to be elastic. The mechanical parameters for the Prony series Maxwell models are given in Table 1.
Table 1: Viscoelastic mechanical properties given in terms of a Prony series
| Material parameter | Symbol | Value |
|---|---|---|
| Young's modulus 1 | \(E_1\) | \(2.93\) GPa |
| Young's modulus 2 | \(E_2\) | \(5.86\) GPa |
| Young's modulus 3 | \(E_3\) | \(6.60\) GPa |
| Young's modulus 4 | \(E_4\) | \(18.32\) GPa |
| Relaxation time 1 | \(\tau_1\) | \(30\) s |
| Relaxation time 2 | \(\tau_2\) | \(300\) s |
| Relaxation time 3 | \(\tau_3\) | \(3000\) s |
| Relaxation time 4 | \(\tau_4\) | \(12000\) s |
| Relaxed Young's modulus | \(E_{\infty}\) | \(39.58\) GPa |
| Poisson's ratio | \(\nu\) | \(0.33\) |
The inner surface of the tube is displaced \(1\) µm in the radial direction. To mimic the displacement occurring instantaneously, it is applied within the first time step. The outer surface of the tube is traction-free. The case is solved over a period of \(7000\) s with a time step of \(800\) s. Inertia and gravity terms are neglected, and the problem is solved as a plane strain. The cylinder is discretised with \(1,152\) cells: \(24\) cells in the radial direction and \(48\) cells in the circumferential direction.
![Figure 1: Problem geometry [1]](/tutorials/more-tutorials/solid-mechanics/viscoelasticity/images/viscoTube-geometry.png) Figure 1: Problem geometry [1]
Figure 1: Problem geometry [1]
Expected Results
In Cardiff et al. [1], the predicted radial stress and radial displacement on the inner tube surface are compared with results from commercial finite element software Abaqus. To illustrate the effect of loading increment size on the employed material law integration, four separate time step sizes are examined (\(700\), \(350\), \(175\), and \(87.5\) s). From Figure 2, one can see that the predicted stresses and displacements are relatively insensitive to time-step size. As the step size is reduced, the predictions are seen to approach the reference finite element solution ("Abaqus FE").
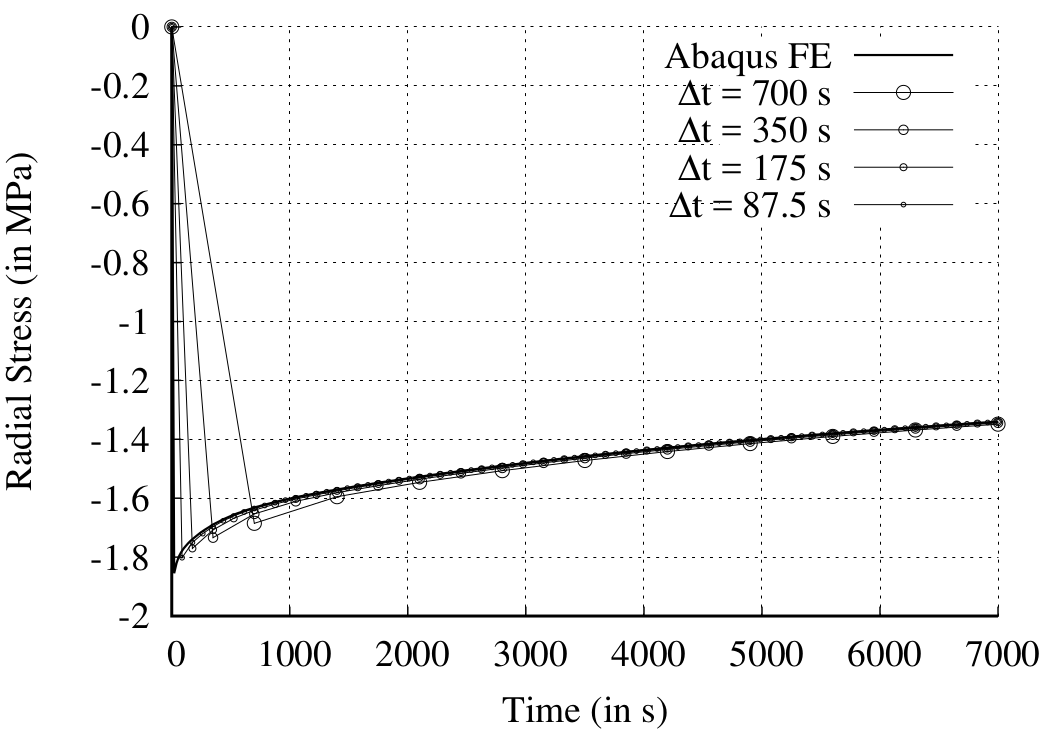 ![Radial displacement]./images/viscoTube-radialDisplacement.png) Figure 2: Radial stress and radial displacement predictions across the wall thickness, showing the effect of loading step size [1]. Comparison is given with finite element results from Abaqus ("Abaqus FE")
![Radial displacement]./images/viscoTube-radialDisplacement.png) Figure 2: Radial stress and radial displacement predictions across the wall thickness, showing the effect of loading step size [1]. Comparison is given with finite element results from Abaqus ("Abaqus FE")
The above plots can be easily reproduced using post-processing function objects added to controlDict. For the chosen point in the domain, the solidPointStress function object is used to write the corresponding stress tensor and the solidPointDisplacement fuction object to write displacement values.
functions
{
pointStressSymmy
{
type solidPointStress;
point (0.0075 0 0);
}
pointStressSymmx
{
type solidPointStress;
point (0 0.0075 0);
}
pointDisp
{
type solidPointDisplacement;
point (0.0075 0 0);
}
}
Running the Case
The tutorial case is located at solids4foam/tutorials/solids/viscoelasticity/viscoTube. The case can be run using the included Allrun script, i.e. > ./Allrun. In this case, the Allrun creates the mesh using blockMesh (> blockMesh) followed by solids4Foam solver (> solids4Foam).
Regression Testing
The viscoTube case also includes a lightweight physics-based regression test (regressionTest.sh). This script automatically runs the case and checks the values for maximum stress and strain are as expected.
This regression test is primarily intended for automated verification (e.g. continuous integration and solver development) rather than routine tutorial usage, and can be run manually with
./regressionTest.sh