Lid-driven cavity flow with a hot wall: thermalCavity
Prepared by Željko Tuković and Philip Cardiff
Tutorial Aims
- Demonstrates how to perform a thermal conjugate heat transfer analysis.
Case Overview
This case extends the traditional OpenFOAM cavity tutorial to include a coupled thermal analysis. The right wall of the cavity is assumed to be elastic and initially hotter than the cavity fluid (Figure 1). A coupled thermo interaction (conjugate heat transfer) analysis is performed where the heat equation is solved in the fluid and solid regions in addition to the Navier-Stokes equations in the fluid. The deformation is not calculated in the solid (for a thermo-fluid-solid interaction tutorial, see the hotTJunction case). The coupling procedure enforces temperature and heat flux continuity at the fluid-solid interface. The right boundary of the solid is heated, causing the solid's temperature to increase, transferring heat to the fluid domain. Within the fluid, the temperature differences generate forces that drive fluid flow.
At time \(t = 0\), the fluid temperature is \(283\) K, whereas the solid temperature is \(323\) K. The fluid domain's top left, and bottom boundaries are assumed to be stationary no-slip walls. The left of the fluid boundary is held at a fixed temperature of \(283\) K, while the right of the solid is held at \(323\) K. All other external boundaries are assumed to be adiabatic (zero heat flux). The right of the fluid domain and the left of the solid domain represent the fluid-solid thermal interface, where thermal constraints (temperature and heat flux continuity) are enforced. In the fluid domain, gravity is assumed to act in the negative vertical direction \((0\;\)-\(9.81\; 0)\) m/s\(^{2}\) and thermal inertial effects are included. The end time is \(10\) s and time-step size \(\Delta t = 0.01\) s.
Figure 1: Problem geometry and initial conditions
The assumed fluid and solid physical parameters are given in Table 1.
Table 1: Physical Parameters
| Parameter | Symbol | Value |
|---|---|---|
| Solid Density | \(\rho\) | 1 kg m\(^{-3}\) |
| Solid Coefficient of Thermal | \(\alpha\) | \(1\times10^{-5}\) K\(^{-1}\) |
| Expansion | ||
| Solid Thermal Conductivity | \(k\) | \(0.04\) W/(m K) |
| Solid Specific Heat Capacity | \(C_p\) | \(1010\) J/(kg K) |
| Fluid Viscosity | \(\mu\) | 0.001 Pa s |
| Fluid Density | \(\rho\) | 1 kg m\(^{-3}\) |
| Fluid Coefficient of Thermal | \(\beta\) | \(2.85\times10^{-3}\) K\(^{-1}\) |
| Expansion | ||
| Fluid Thermal Conductivity | \(\lambda\) | \(0.03\) W/(m K) |
| Fluid Specific Heat Capacity | \(C_p\) | \(1010\) J/(kg K) |
| Fluid Reference Temperature | \(T_{ref}\) | \(303\) K |
| Fluid Turbulent Prandtl No. | \(\text{Pr}_t\) | 0.85 |
| Gravity | \(g\) | \((0 \;\)-\(9.81 \; 0)\) m \(s^{-2}\) |
Results
Over the duration of the simulation, the solid heats the fluid, causing a thermal circulation to form in the fluid. The evolution of the temperature of velocity fields is shown in Video 1. The temperature distribution at \(t = 10\) s is shown in Figure 2.
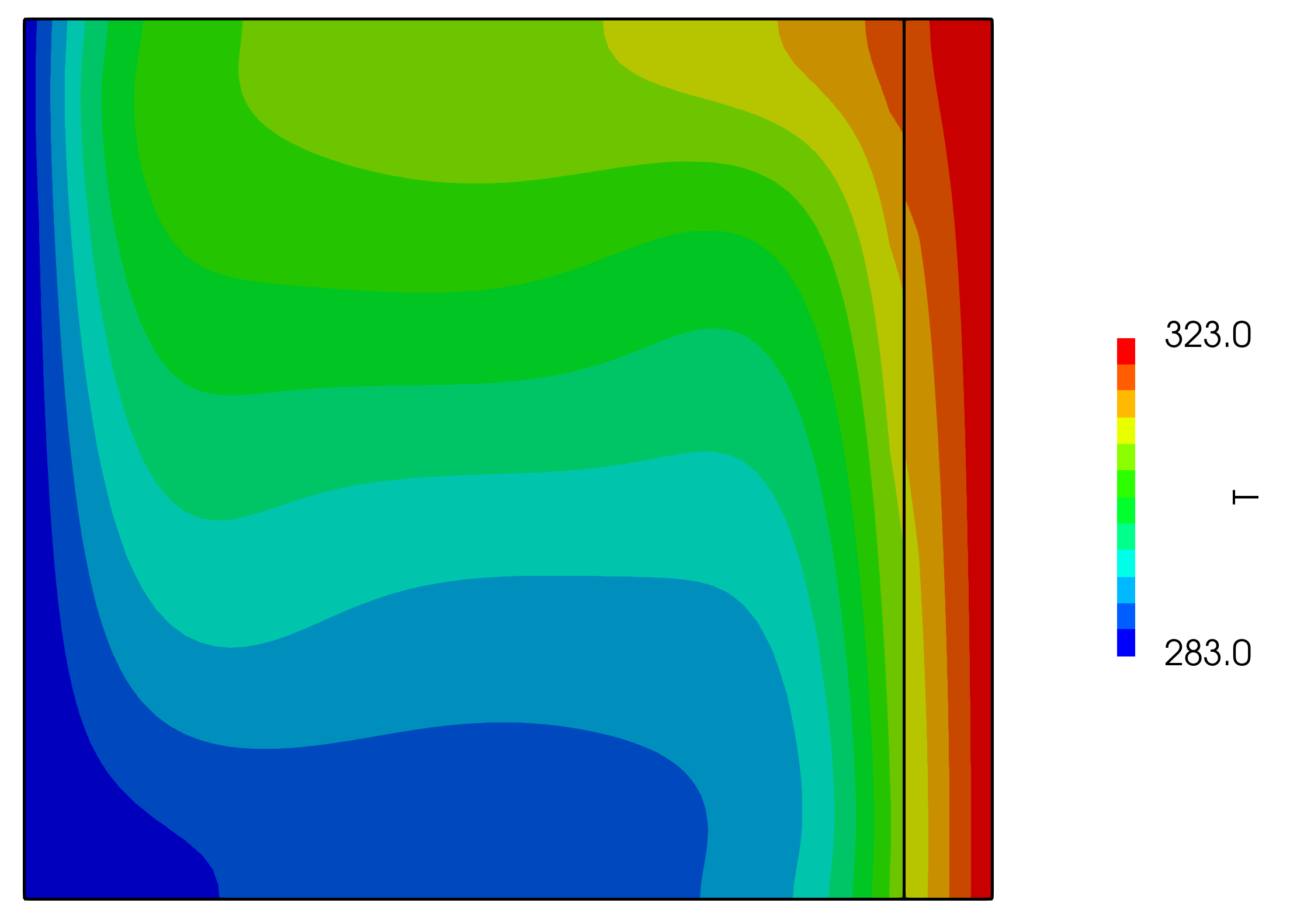Figure 2: Temperature distribution at the end time
Video 1: Evolution of the temperature and velocity distributions within the fluid and solid domains
Running the Case
The tutorial case is located at solids4foam/tutorials/thermofluidSolidInteraction/thermalCavity. The case can be run using the included Allrun script, i.e. > ./Allrun. The Allrun script first executes blockMesh for both solid and fluid domains (> blockMesh -region fluid and > blockMesh -region solid ), and the solids4foam solver is used to run the case (> solids4Foam).