Internally pressurised bi-material thick-walled cylinder: `layeredPipe`

Prepared by Željko Tukovic, Philip Cardiff and Ivan Batistić

Tutorial Aims

Demonstrate the solution of a multi-material solid mechanics problem;
Compare the accuracy of a solid model against the available analytical solution.

Case Overview

In this case, an internally pressurised bi-material thick-walled cylinder is analysed (Figure 1). The problem is considered plane stress, with a quarter of the domain modelled because of symmetry. The case is simulated as a steady state using one loading step. The outside surface is modelled as stress-free, and the left and bottom boundaries are symmetry planes. The inner bore surface has a prescribed constant pressure \(p_i=1\times 10^5\) Pa. The inner material (region 1 in Figure 1) has a Poisson's ratio of \(\nu_1=0.35\) and a Young's modulus of \(E_1 = 20\) GPa, while the outer material (region 2 in Figure 1) has a Poisson's ratio of \(\nu_2=0.3\) and a Young's modulus of \(E_2 = 200\) GPa; this results in an order of magnitude difference between the Young's modulii, i.e., \(E_2/E_1=10\). The number of cells is set to \(120\) circumferentially and \(50\) radially.

Figure 1: Problem geometry [1]

Figure 1 - Problem geometry [1]

Expected Results

Comparison between numerical and analytical solutions is performed in terms of circumferential and radial stresses in the radial direction through the cylinder, for which the analytical solutions are as follows [1]:

\[\sigma_r = \frac{r_1^2p_i-r_2^2p_{12}+(p_{12}-p_i)\left(\dfrac{r_1r_2}{r}\right)^2}{r_2^2-r _1^2} \qquad \text{for } r_1 \leq r < r_2,\] \[\sigma_r = \frac{r_2^2p_{12}-p_{12}\left(\dfrac{r_2r_3}{r}\right)^2}{r_3^2-r_2^2} \qquad \text{for } r_2 < r \leq r_3,\] \[\sigma_{\theta} = \frac{r_1^2p_i-r_2^2p_{12}-(p_{12}-p_i)\left(\dfrac{r_1r_2}{r}\right)^2}{r_2^2-r _1^2} \qquad \text{for } r_1 \leq r < r_2,\] \[\sigma_{\theta} = \frac{r_2^2p_{12}+p_{12}\left(\dfrac{r_2r_3}{r}\right)^2}{r_3^2-r_2^2} \qquad \text{for } r_2 < r \leq r_3,\]

where the pressure at the interface, \(p_{12}\) is given as follows:

\[p_{12}=\dfrac{\dfrac{2r_1^2p_i}{E_1(r_2^2-r_1^2)}}{\dfrac{1}{E_2}\left(\dfrac{r_ 3^2+r_2^2}{r_3^2-r_2^2}+\nu_2 \right) + \dfrac{1}{E_1}\left(\dfrac{r_2^2+r_1^2}{r_2^2-r_1^2}-\nu_1 \right)}.\]

Figures 2 and 3 show a comparison between the analytical and numerical solutions of radial \(\sigma_r\) and circumferential \(\sigma_{\theta}\) stress distributions. One can see that the numerical solution closely matches the analytical one.

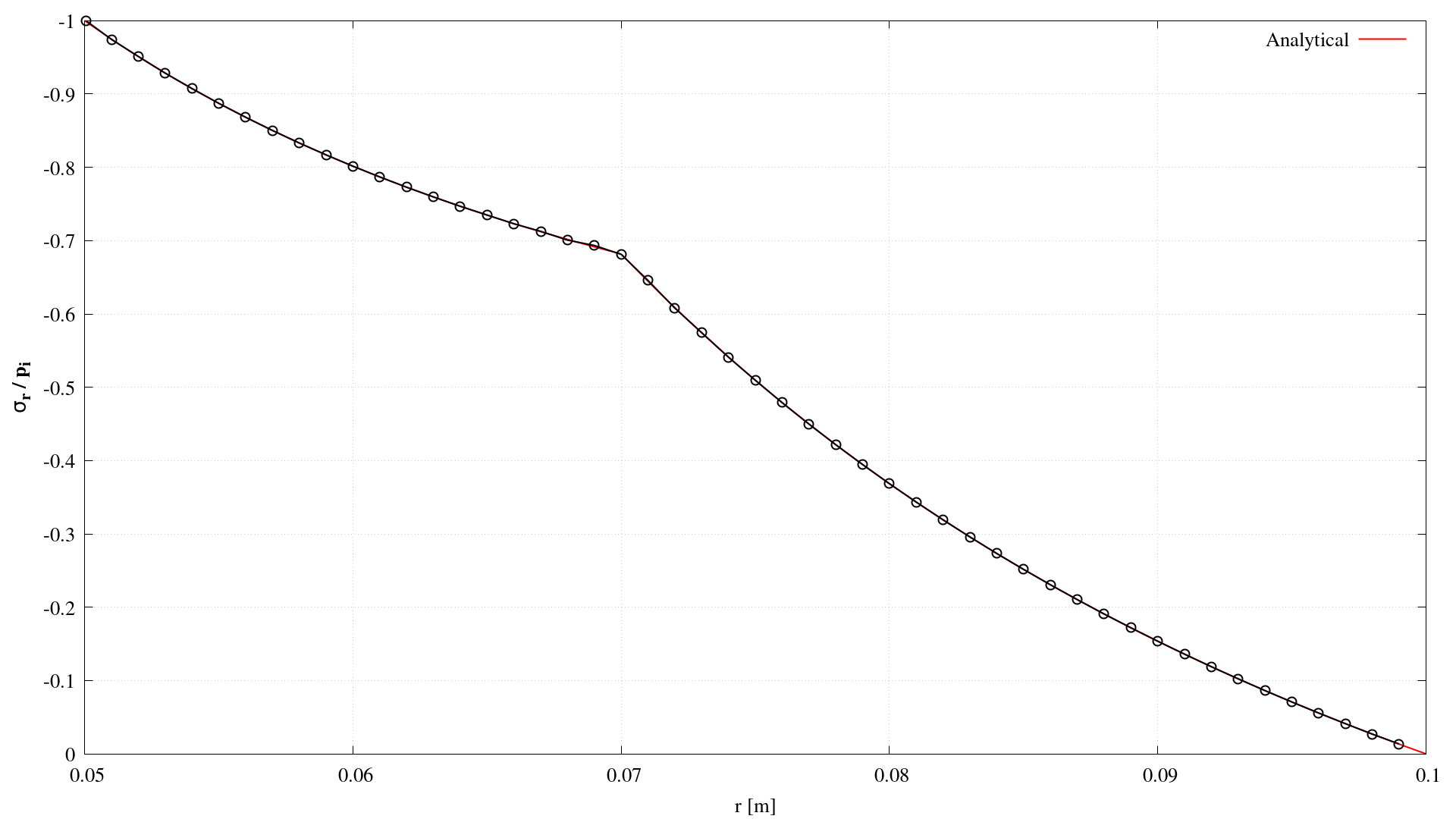
Figure 2: Comparison of numerical (circles) and analytical (line) radial stress distributions

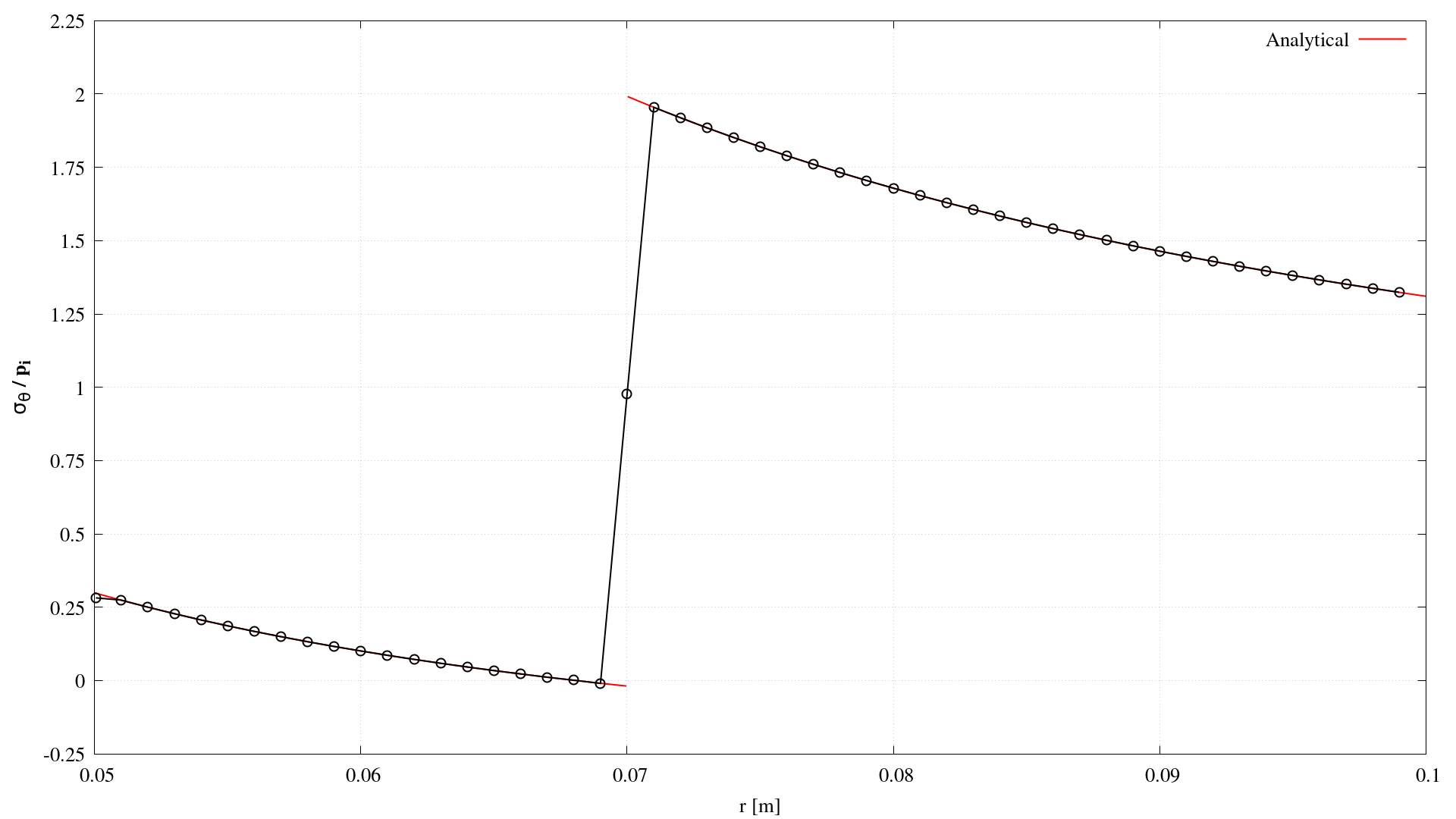
Figure 3: Comparison of numerical (circles) and analytical (line) circumferential stress distributions

The plots above are created automatically within the Allrun script using sample utility and gnuplot. The transformStressToCylindrical function object in system/controlDict is used to transform the \(\sigma\) stress tensor from Cartesian coordinates to the cylindrical:

functions
{
    transformStressToCylindrical
    {
        type        transformStressToCylindrical;
        origin      (0 0 0);
        axis        (0 0 1);
    }
}
  

The cylindrical stresses (sigma:Transformed) are plotted along a \(\theta=45^{\circ}\) line using the sample utility:

fields( sigma:Transformed );

sets
(
    line
    {
        type       face;
        axis       distance;
        start      (0.0 0.0 0.0005);
        end        (0.07 0.07 0.0005);
    }
);
  

Running the Case

The tutorial case is located at solids4foam/tutorials/solids/multiMaterial/layeredPipe. The case can be run using the included Allrun script, i.e. > ./Allrun. In this case, the Allrun creates the mesh using blockMesh (> blockMesh) followed by calls to the setSet and setsToZones utilities to create cell zones for inner and outer cylinder materials. After that, the case is run with the solids4Foam solver (> solids4Foam). As the last step, the sample utility is used to extract data. Optionally, if gnuplot is installed, the radial and circumferential stress distributions are plotted in the sigmaR.png and sigmaTheta.png files.

Note

For multi-material cases, solids4foam expects to find a cellZone for eachmaterial defined in constant/mechanicalProperties, where the cellZone name isassumed to be the same as the material name in constant/mechanicalProperties.

References

[1] Ž. Tuković, A. Ivanković, and A. Karač, "Finite-volume stress analysis in multi-material linear elastic body," International Journal for Numerical Methods in Engineering, vol. 93, no. 4, pp. 400–419, 2013.

Internally pressurised bi-material thick-walled cylinder: layeredPipe