Internally pressurised thick-walled cylinder: pressurisedCylinder
Prepared by Iago Lessa de Oliveira, Ivan Batistić and Philip Cardiff
Tutorial Aims
- Demonstrate the solver accuracy for a compressible linear elastic test case;
- Examine the solver performance when approaching the incompressibility limit.
Case Overview
In this case, a homogeneous thick-wall cylindrical pressure vessel with an inner radius \(r_i = 7\) m, outer radius \(R_o = 18.625\) m, and loaded internally with pressure \(p = 100\) MPa is analysed. The material is considered linear elastic with Young modulus \(E=10\) GPa and Poisson's ratio \(\nu=0.3\). The problem is considered plane stress, with the 2-D computational domain comprising a quarter of the cylinder geometry. The cylinder is discretised with \(900\) cells: \(30\) cells in the radial and \(30\) in the circumferential direction. Gravitational and inertial effects are neglected, and the case is solved using one loading increment.
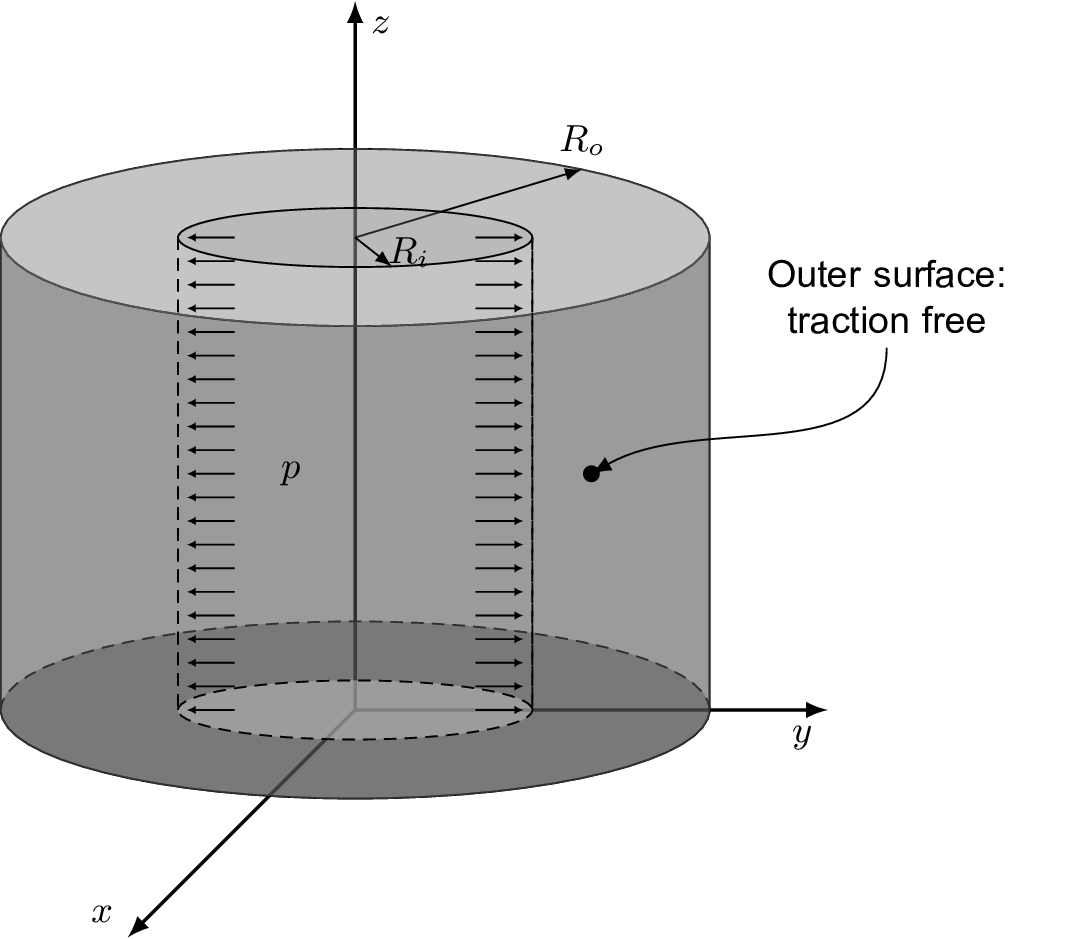
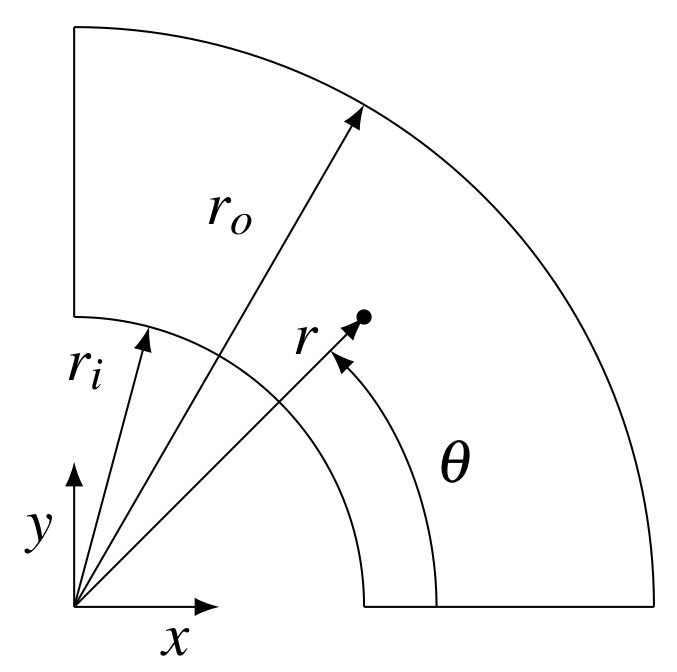
Figure 1 - Problem geometry
Results
The analytical solution for the stress field is [1]:
\[\sigma_r = p \dfrac{r_i^2}{r_o^2-r_i^2}\left(1-\dfrac{r_o^2}{r^2}\right),\] \[\sigma_{\theta} = p \dfrac{r_i^2}{r_o^2-r_i^2}\left(1+\dfrac{r_o^2}{r^2}\right),\] \[\sigma_{z} = 0,\]and for radial displacement:
\[u_r = \dfrac{p}{E}\dfrac{r_i^2}{r_o^2-r_i^2}\left[(1-\nu)r+(1+\nu)\dfrac{r_o^2}{r}\rig ht].\]Results presented in Figures 2 and 3 show numerical and analytical calculations of radial displacement \(u_r\), circumferential \(\sigma_{\theta}\) and radial \(\sigma_r\) stress, showing good agreement. The plotting script plot.gnuplot automatically generates these diagrams when running the Allrun script; however, note that geometry and material properties are hardcoded in the plot.gnuplot script:
Ri = 7 # Inner cylinder radius
Ro = 18.625 # Outer cylinder radius
E = 1e10 # Young modulus
p = 10e6 # Internal pressure
nu = 0.3 # Poissons ratio
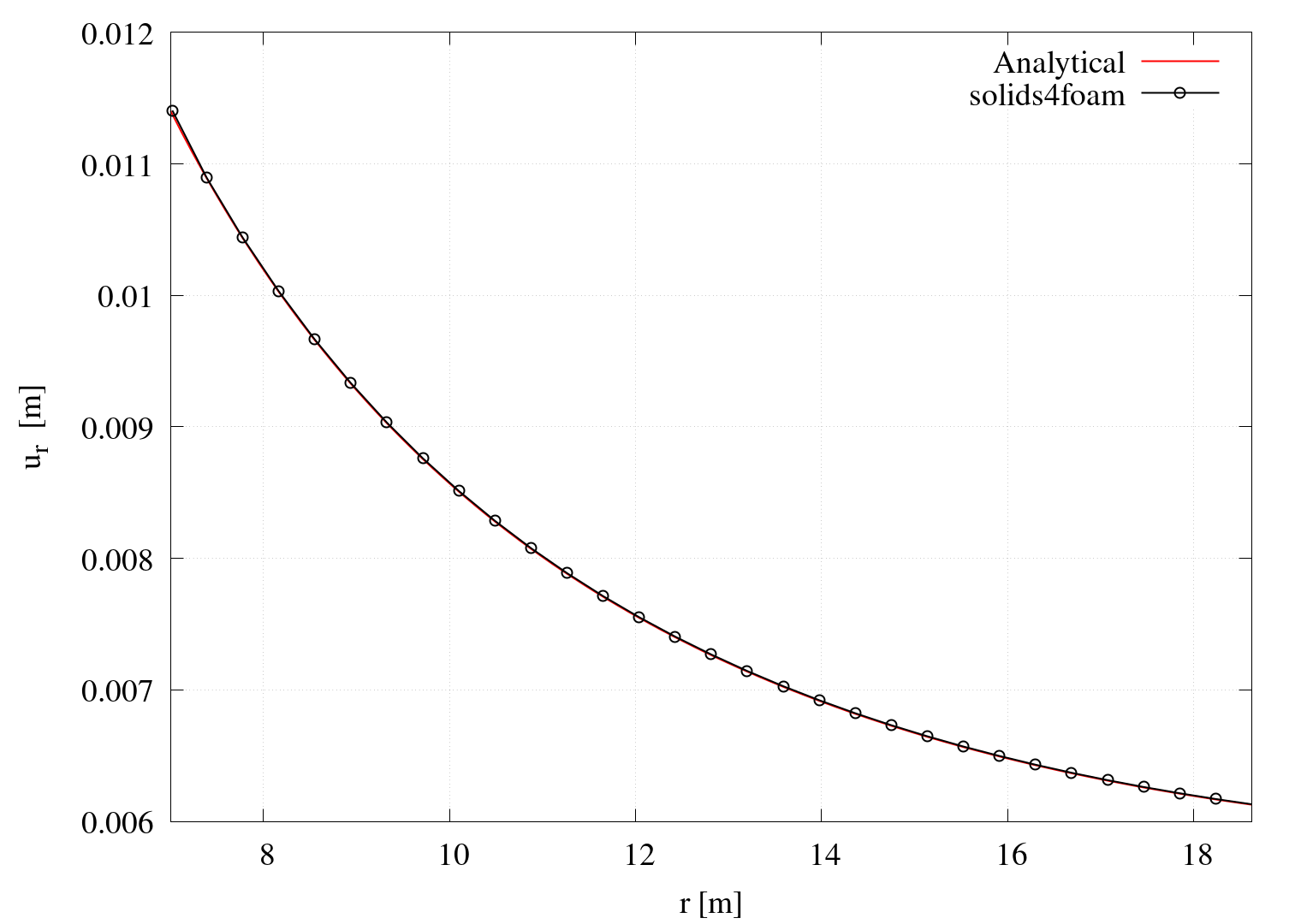
Figure 2: Distribution of the radial displacement across cylinder thickness
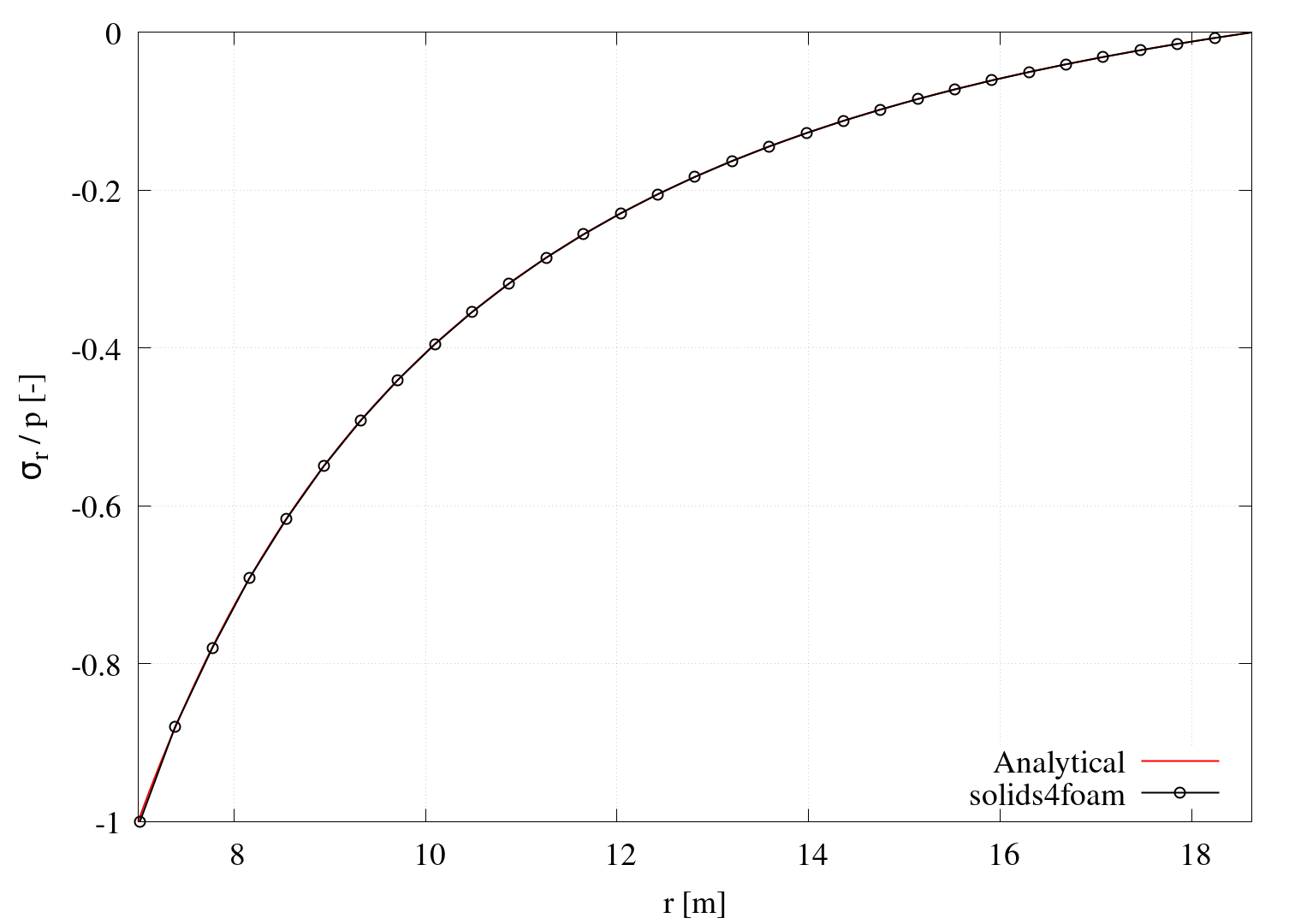
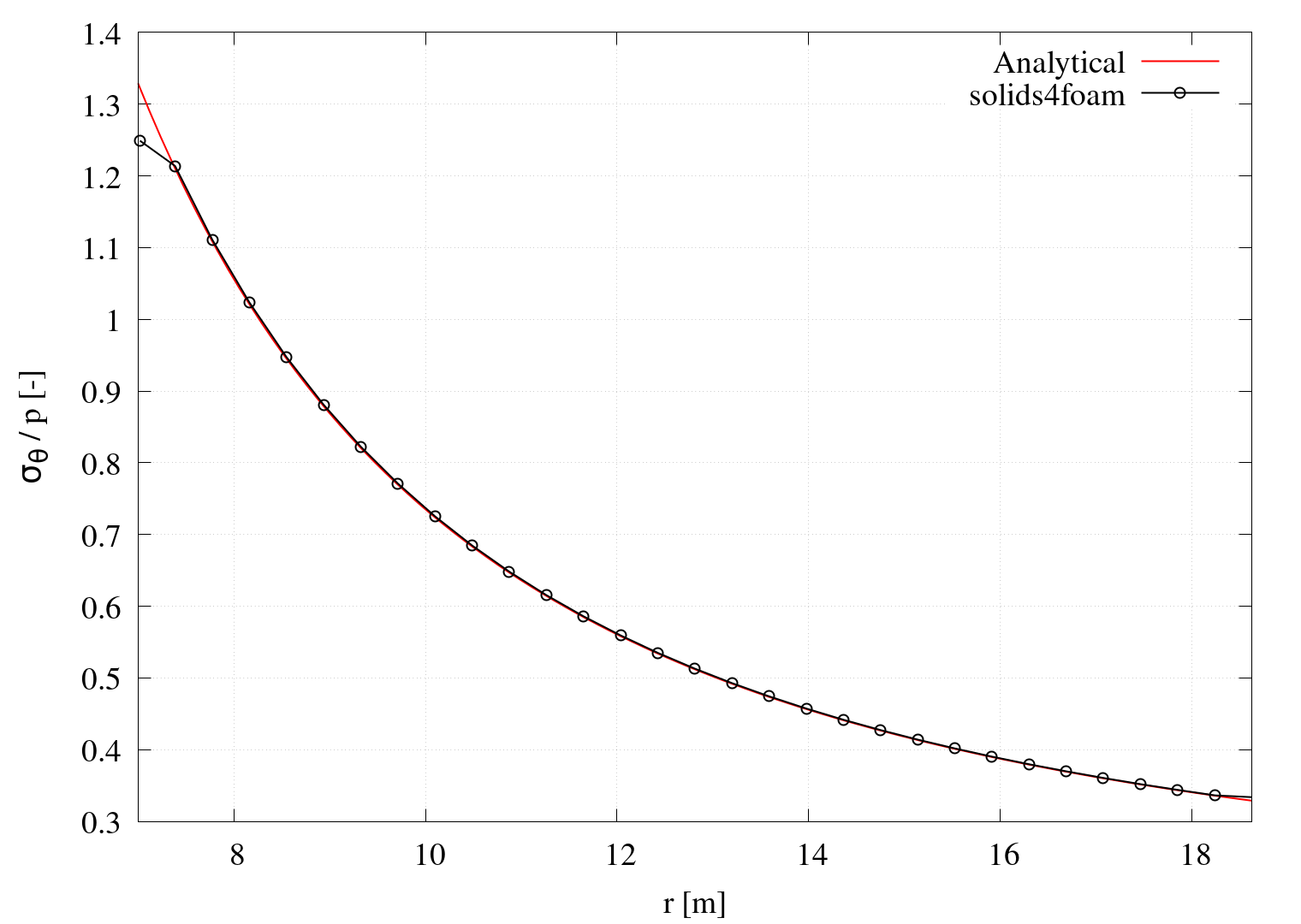
Figure 3 - Distribution of the circumferential and radial stress across cylinder thickness
Approaching the Incompressibility Limit
Formulating the governing momentum balance with the displacement variable as the only dependent variable has limitations in modelling incompressible materials. Specifically, the formulation exhibits efficiency degradation and volumetric locking while approaching Poisson's ratio of \(0.5\). An appropriate formulation for these problems is a pressure-displacement (mixed) formulation, in which the constitutive relation is defined via two unknowns (displacement and pressure).
From Figures 4 and 5, one can see what happens with the resulting stress field when the displacement-based formulation is used to model nearly incompressible material (\(\nu=0.495\)). As expected, the stress distribution exhibits oscillatory behaviour.
Note that for the analysed case, stresses are not a function of material properties (Young's modulus and Poisson's ratio) because of the plane stress condition (\(\sigma_{zz}=0\)). Accordingly, the case is solved with a plane strain assumption (\(\varepsilon_{zz}=0\)) to generate these plots.
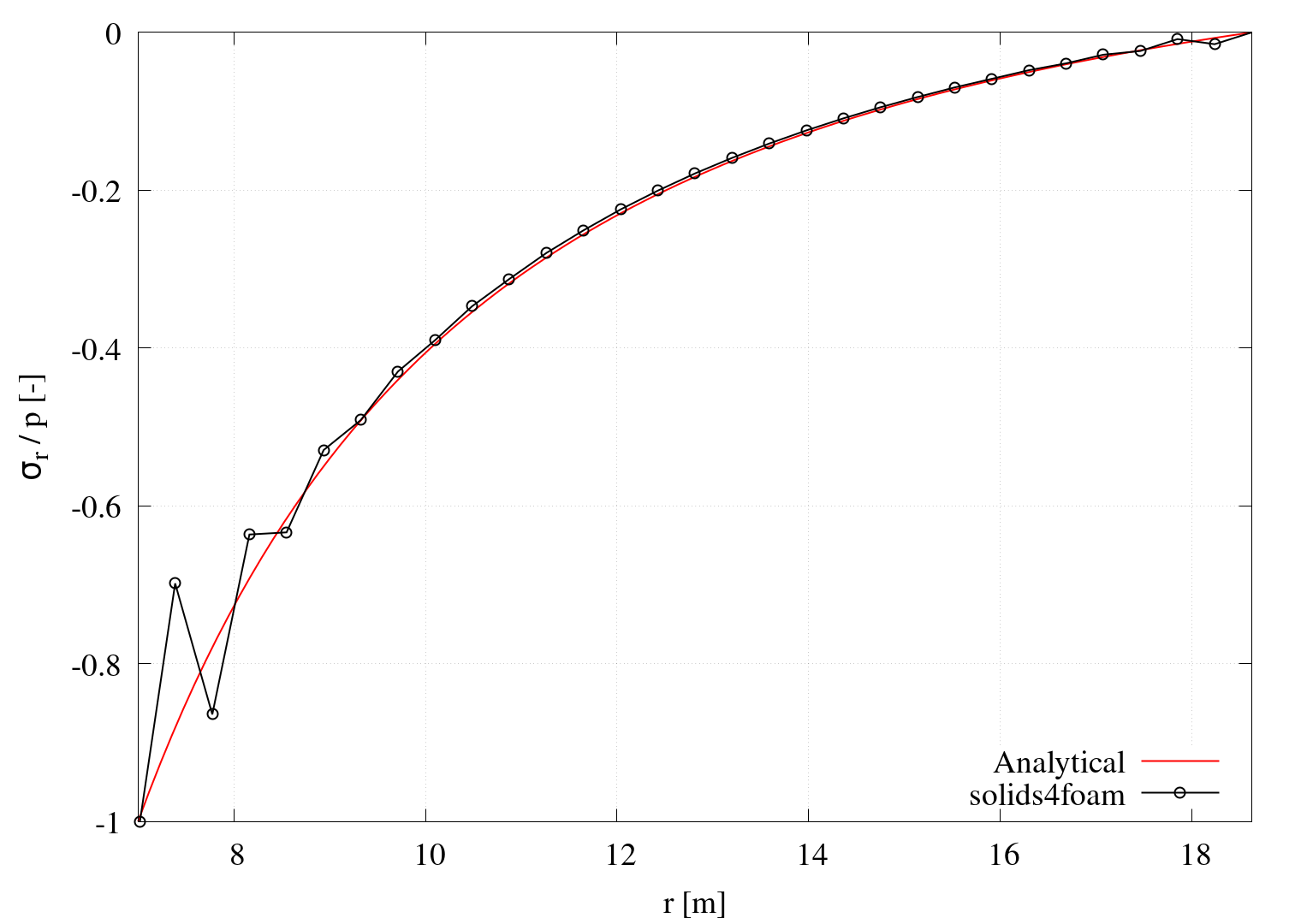
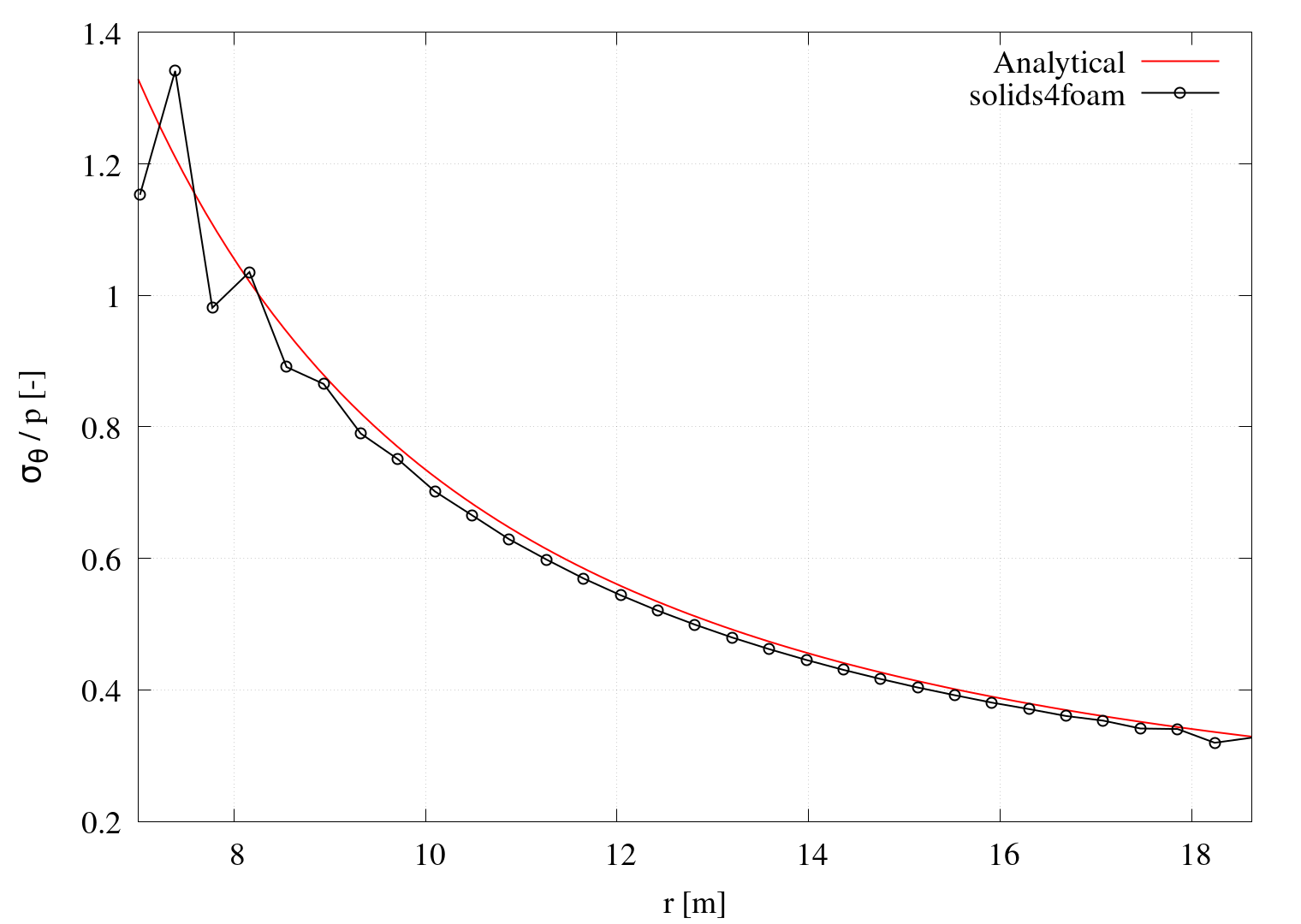
Figure 3 - Distribution of the circumferential and radial stress across cylinder thickness
Running the Case
The tutorial case is located at solids4foam/tutorials/solids/linearElasticity/pressurisedCylinder. The case can be run using the included Allrun script, i.e. > ./Allrun. In this case, the Allrun consists of creating the mesh using blockMesh (> ./blockMesh) followed by running the solids4foam solver (> ./solids4Foam) and > ./sample utility. Optionally, if gnuplot is installed, the radial and circumferential stress distribution together with the profile of radial displacement are plotted in the sigmaR.png, sigmaTheta.png and dispR.png files.
The same case is solved with Mooney-Rivlin hyperelastic material and can befound in the solids/hyperelasticity/cylindricalPressureVessel. Thehyperelastic case was initially proposed by Bijelonja et al. [2,3].
References
[1] J. G. S.P. Timoshenko, Theory of Elasticity. McGraw-Hill, New York, 1970.